Magnitudes Físicas : 2012

martes, 14 de agosto de 2012

trabajo y energía, movimientos oscilatorios

Trabajo efectuado por una fuerza constante.

En mecánica, el trabajo que realiza una fuerza sobre un cuerpo equivale a la energía necesaria para desplazar este cuerpo. El trabajo es una magnitud física escalar que se representa con la letra $\ W$ (del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el sistema internacional de medidas. El concepto de trabajo es el mismo sin importar el tipo de fuerza que lo realice. Pero la forma de calcularlo es lo que cambia bastante.
Si la fuerza es constante, aplicamos esta ecuación directamente T = F*d*cos a, siendo a el ángulo entre F y d. Si la fuerza es variable tenés que calcular mediante una integral o si conocés cómo cambia la fuerza en función de la distancia recorrida, gráfica F = f(d), tenés que calcular el área bajo la curva de esa gráfica y habrás encontrado el trabajo.

Producto escalar de dos vectores

El producto escalar de vectores se puede definir de dos maneras equivalentes, una manera algebraica, y otra geométrica. Comenzaremos con la manera geométrica, que tiene un significado intuitivo.
Tomemos dos vectores $\vec a$ y $\vec b$ , y llamemos $\alpha$ al ángulo que ellos forman. Entonces, el producto escalar entre dichos vectores es:

$\begin{displaymath} \vec a \cdot \vec b = \vert\vec a \vert \vert\vec b \vert cos (\alpha), \end{displaymath}$

en que $\vert\vec a\vert$ y $\vert\vec b\vert$ corresponden a las longitudes de los vectores $\vec a$ y $\vec b$ , respectivamente. Naturalmente, debe cumplirse que

$\begin{displaymath} \vec a \cdot \vec a = \vert\vec a \vert^2. \end{displaymath}$

Si usamos la representación cartesiana, se tiene que:

$\begin{displaymath} \vert\vec a \vert^2 = a_x^2 + a_y^2 + a_z^2, \end{displaymath}$

www.youtube.com/watch?v=iME76KcwJWg

Energía cinética

Cuando un cuerpo está en movimiento posee energía cinética ya que al chocar contra otro puede mover lo y, por lo tanto, producir un trabajo.

Para que un cuerpo adquiera energía cinética o de movimiento; es decir, para ponerlo en movimiento, es necesario aplicarle una fuerza. Cuanto mayor sea el tiempo que esté actuando dicha fuerza, mayor será la velocidad del cuerpo y, por lo tanto, su energía cinética será también mayor.Otro factor que influye en la energía cinética es la masa del cuerpo.

Energía potencial

se conoce como energía potencial a la capacidad que tiene un cuerpo para desarrollar una acción de acuerdo a cómo están configurados en el sistema de cuerpos que realizan fuerza entre sí. En otras palabras, la energía potencial es la energía que es capaz de generar un trabajo como consecuencia de la posición del cuerpo.

www.fisicavideos1.blogspot.com/.../trabajo-y-energia-teoria-y-ejercicios.ht...

Teorema del trabajo y la energía

El trabajo, por sus unidades, es una forma de transferencia o cambio en la energía: cambia la posición de una partícula (la partícula se mueve). Éste cambio en la energía se mide a partir de todos los efectos que la partícula sufre, para el trabajo, los efectos son todas las fuerzas que se aplican sobre ella (trabajo neto o trabajo total Wt).

El teorema del trabajo y la energía relaciona éstos dos conceptos:

El trabajo efectuado por la fuerza neta sobre una partícula es igual al cambio de energía cinética de la partícula *:

W = ∆K = K(2) - K(1)

Éste teorema facilita muchos cálculos de problemas que involucran éstas propiedades.

Energía mecánica y su conservación

La energía es la capacidad de la materia para producir transformaciones.

La energía mecánica que ya definiremos más adelante, es la que nos permite realizar trabajo mecánico.

Trabajo mecánico

Aunque en la vida cotidiana es compón asociar la idea de trabajo con el esfuerzo o cualquier otra acción en la que se requiera energía, en física y en mecánica en particular, el trabajo tiene una definición bastante restringida. Decimos que una fuerza realiza trabajo sobre un cuerpo cuando al actuar sobre éste lo desplaza en la misma dirección en que actúa. Por ejemplo: En este caso, la fuerza realiza trabajo porque el cuerpo es desplazado una distancia d de manera paralela a la fuerza.

Operacional mente el trabajo (W) se determina como:

W = F∙d

Sus unidades están dadas por:

W = F∙dà [N∙m]= joule =[J]

La energía mecánica (EM) de un cuerpo o un sistema, equivale a la suma de sus energías potencial y cinpetica, es decir:

EM = EC + EP

La importancia de la energía mecánica, se debe a que es una magnitud que al igual que el momentum se conserva constante en situaciones en que no hay fuerzas externas actuando sobre el sistema y en ausencia de roce.

Es decir:

EC + EP = Constante

Esta ley es mucho más fácil comprenderla a través de un ejemplo:

Una piedra se suelta desde una altura de 2 m respecto del suelo aquí, en la superficie terrestre. Si despreciamos los efectos de roce con el aire, ¿con qué rapidez impacta en el suelo?

Cambios de la energía mecánica cuando se presenta una fuerza no conservativa

Complementando el buen aporte de Julio, podés mencionar que el nombre se refiere a que afectan o no la conservación de la energía mecánica total.
Las fuerzas que no afectan la conservación de la energía son conservativas, son ejemplos la fuerza gravitacional y la de origen electromagnético.

Son NO conservativas las que hacen que NO se conserve la energía total. Es típica de los rozamientos. Las fuerzas de rozamiento realizan trabajo en contra del movimiento de los cuerpos (para que se realice un trabajo, como recordarás, además de la fuerza que lo realiza debe haber un desplazamiento). Ese trabajo es energía que se le resta al cuerpo, y se disipa, por ejemplo en calor, siendo irreversible (no es energía que pueda volver al cuerpo).

Un ejemplo `típico de la interacción de estas fuerzas y las energías puestas en juego podés verlo en una montaña rusa.

Un carrito es elevado desde la base por medio de un medio mecánico, se le entrega energía potencial:
Epo = m g h
Supongamos que esa es su energía total en el punto más alto, quiere decir que la Ec (cinética) momentáneamente es cero (despreciamos la pequeña velocidad de transición entre el ascenso mecánico y el inicio del descenso, con lo cual ahí arriba, en el inicio del descenso es:
Ec = 0.5 m vo² =0 aprox.).

Etotal = E = Epo + Eco = Epo + 0 = m g h

Si no hubiese rozamiento alguno al bajar por gravedad (el peso del carrito es la fuerza gravitacional) iría ganando velocidad tal que:

E = cte = m g y + ½ m v²

y es la altura intermedia (entre 0 y h) y lo que "pierde" en la energía potencial lo gana en energía cinética.

En tal caso el carrito podría llegar siempre a la misma altura inicial en virtud del impulso que gana con la velocidad, ... a mayor altura, menor velocidad, a menor altura, mayor velocidad, pero... pero el rozamiento existe, y tanto en los ejes del carro, como en la frotación con el aire, como resistencias en el contacto ruedas-rieles, se genera trabajo de las fuerzas NO conservativas o disipativas (es lo mismo) intervinientes. que le quitan energía al carrito, entonces su energía en el tiempo estará dada por:

Ecarrito = Epo + Eco - Trabajo de las fuerzas disipativas (que a lo largo del recorrido tendrán intensidades variables y no se pueden expresar en una fórmula simple)

Ecarrito = Eo - Wr = m g h - Wr

Eo = Epo es la energía total iniaial en el punto más alto,
Wr = trabajo de las fuerzas no conservativas

Sólo me falta agregar que en tramo final se frena totalmente al carrito, o sea que se realiza un trabajo que le drena o resta toda la energía cinética que le quedaba (cinética, porque estando al nivel del piso considero ya que Epfinal = 0).

MOVIMIENTOS OSCILATORIOS

Movimiento armónico simple

El movimiento armónico simple (se abrevia m.a.s.), también denominado movimiento vibratorio armónico simple (abreviado m.v.a.s.), es un movimiento periódico, oscilatorio y vibratorio en ausencia de fricción, producido por la acción de una fuerza recuperadora que es directamente proporcional al desplazamiento pero en sentido opuesto.Y que queda descrito en función del tiempo por una función senoidal (seno o coseno). Si la descripción de un movimiento requiriese más de una función armónica, en general sería un movimiento armónico, pero no un m.a.s.
En el caso de que la trayectoria sea rectilínea, la partícula que realiza un m.a.s. oscila alejándose y acercándose de un punto, situado en el centro de su trayectoria, de tal manera que su posición en función del tiempo con respecto a ese punto es una sinusoide. En este movimiento, la fuerza que actúa sobre la partícula es proporcional a su desplazamiento respecto a dicho punto y dirigida hacia éste.

masa unida a un resorte

Movimiento Armónico Simple es el masa - resorte que consiste en una masa “m” unida a un resorte, que a su vez se halla fijo a una pared, como se muestra en la figura. Se supone movimiento sin rozamiento sobre la superficie horizontal.El resorte es un elemento muy común en máquinas. Tiene una longitud normal, en ausencia de fuerzas externas. Cuando se le aplican fuerzas se deforma alargándose o acortándose en una magnitud “x” llamada “deformación”. Cada resorte se caracteriza mediante una constante “k” que es igual a la fuerza por unidad de deformación que hay que aplicarle. La fuerza que ejercerá el resorte es igual y opuesta a la fuerza externa aplicada (si el resorte deformado está en reposo) y se llama fuerza recuperadora elástica.

Dicha fuerza recuperadora elástica es igual a :

F= - K . X

oscilador armónico simple

El oscilador armónico es uno de los sistemas más estudiados en la física, ya que todo sistema que oscila al rededor de un punto de equilibrio estable se puede estudiar en primera aproximación como si fuera un oscilador.

La característica principal de un oscilador armónico es que está sometido a una fuerza recuperadora, que tiende a devolverlo al punto de equilibrio estable, con una intensidad proporcional a la separación respecto de dicho punto,

$\displaystyle F = - k ( x - x_0 ) \ ,$

(1)

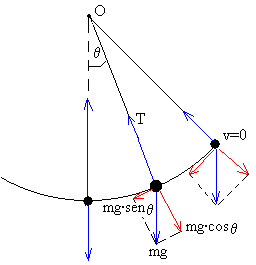
donde k es la constante de recuperación, y

es la posición de equilibrio, que sin pérdida de generalidad podemos tomar

. La fuerza recuperadora es conservativa, por lo que tiene asociado una energía potencial,

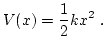
$\displaystyle V(x) = \frac12 k x^2 \ .$

pendulo simple

Un péndulo simple se define como una partícula de masa m suspendida del punto O por un hilo inextensible de longitud l y de masa despreciable.
Si la partícula se desplaza a una posición q₀ (ángulo que hace el hilo con la vertical) y luego se suelta, el péndulo comienza a oscilar.

El péndulo describe una trayectoria circular, un arco de una circunferencia de radio l. Estudiaremos su movimiento en la dirección tangencial y en la dirección normal. Las fuerzas que actúan sobre la partícula de masa m son dos

el peso mg
La tensión T del hilo

Descomponemos el peso en la acción simultánea de dos componentes, mg·senq en la dirección tangencial y mg·cosq en la dirección radial.

Ecuación del movimiento en la dirección radial

La aceleración de la partícula es a_n=v²/l dirigida radialmente hacia el centro de su trayectoria circular.
La segunda ley de Newton se escribe
ma_n=T-mg·cosq
Conocido el valor de la velocidad v en la posición angular q podemos determinar la tensión T del hilo.
La tensión T del hilo es máxima, cuando el péndulo pasa por la posición de equilibrio, T=mg+mv²/l
Es mínima, en los extremos de su trayectoria cuando la velocidad es cero, T=mgcosq₀

Principio de conservación de la energía

En la posición θ=θ₀ el péndulo solamente tiene energía potencial, que se transforma en energía cinética cuando el péndulo pasa por la posición de equilibrio.

trabajo y energía

trabajo efectivo para una fuerza constante

El concepto de trabajo es el mismo sin importar el tipo de fuerza que lo realice. Pero la forma de calcularlo es lo que cambia bastante.
Si la fuerza es constante, aplicamos esta ecuación directamente T = F*d*cos a, siendo a el ángulo entre F y d.
Si la fuerza es variable tenés que calcular mediante una integral o si conocés cómo cambia la fuerza en función de la distancia recorrida, gráfica F = f(d), tenés que calcular el área bajo la curva de esa gráfica y habrás encontrado el trabajo.

www.youtube.com/watch?v=cswT3j-Y6S0

www.julioprofe.net/p/fisica.html

producto escalar de dos vectores

El producto escalar de vectores se puede definir de dos maneras equivalentes, una manera algebraica, y otra geométrica. Comenzaremos con la manera geométrica, que tiene un significado intuitivo.
Tomemos dos vectores $\vec a$ y $\vec b$ , y llamemos $\alpha$ al ángulo que ellos forman. Entonces, el producto escalar entre dichos vectores es:

$\begin{displaymath} \vec a \cdot \vec b = \vert\vec a \vert \vert\vec b \vert cos (\alpha), \end{displaymath}$

en que $\vert\vec a\vert$ y $\vert\vec b\vert$ corresponden a las longitudes de los vectores $\vec a$ y $\vec b$ , respectivamente. Naturalmente, debe cumplirse que

$\begin{displaymath} \vec a \cdot \vec a = \vert\vec a \vert^2. \end{displaymath}$

Si usamos la representación cartesiana, se tiene que:

$\begin{displaymath} \vert\vec a \vert^2 = a_x^2 + a_y^2 + a_z^2, \end{displaymath}$

es decir, se satisface el teorema de Pitágoras, conocido de nuestros estudios de geometía elemental. Indudablemente, la definición del producto escalar de vectores puede usarse para definir el ángulo entre dos vectores,

$\begin{displaymath} cos (\alpha) = \frac{\vec a \cdot \vec b }{\vert\vec a \vert\vert\vec b\vert}. \end{displaymath}$

De acuerdo a la definición dada, es fácil ver que el producto escalar de dos vectores puede tambien definirse usando las componentes cartesianas de los vectores,

$\begin{displaymath} \vec a \cdot \vec b = a_x b_x + a_y b_y + a_z b_z. \end{displaymath}$

energía cinética

Cuando un cuerpo está en movimiento posee energía cinética ya que al chocar contra otro puede moverlo y, por lo tanto, producir un trabajo.
Para que un cuerpo adquiera energía cinética o de movimiento; es decir, para ponerlo en movimiento, es necesario aplicarle una fuerza Cuanto mayor sea el tiempo que esté actuando dicha fuerza, mayor será la velocidad del cuerpo y, por lo tanto, su energía cinética será también mayor.
Otro factor que influye en la energía cinética es la masa del cuerpo.
Por ejemplo, si una bolita de vidrio de 5 gramos de masa avanza hacia nosotros a una velocidad de 2 km / h no se hará ningún esfuerzo por esquivarla. Sin embargo, si con esa misma velocidad avanza hacia nosotros un camión, no se podrá evitar la colisión.
La fórmula que representa la Energía Cinética es la siguiente:

E _c = 1 / 2 • m • v ²

E_c = Energía cinética

m = masa

v = velocidad

Energía potencial

Todo cuerpo que se ubicado a cierta altura del suelo posee energía potencial.
Esta afirmación se comprueba cuando un objeto cae al suelo, siendo capaz de mover o deformar objetos que seencuentren a su paso. El movimiento o deformación será tanto mayor cuanto mayor sea al altura desde la cual cae el objeto.
Otra forma de energía potencial es la que está almacenada en los alimentos, bajo la forma de energía química. Cuando estos alimentos son procesados por nuestro organismo, liberan la energía que tenían almacenada.
Para una misma altura, la energía del cuerpo dependerá de su masa. Aplicando una fuerza, esta energía puede ser transferida de un cuerpo a otro y aparecer como energía cinética o de deformación. Sin embargo, mientras el cuerpo no descienda, la energía no se manifiesta: es energía potencial.
Todos los cuerpos tienen energía potencial que será tanto mayor cuanto mayor sea su altura. Como la existencia de esta energía potencial se debe a la gravitación (fuerza de gravedad), su nombre más completo es energía potencial gravitatoria.

teorema del trabajo y la energía

El teorema del trabajo y la energía relaciona éstos dos conceptos:

El trabajo efectuado por la fuerza neta sobre una partícula es igual al cambio de energía cinética de la partícula *:

W = ∆K = K(2) - K(1)

Éste teorema facilita muchos cálculos de problemas que involucran éstas propiedades.

Ejemplo. Una bala de 20 g choca contra un banco de fango, como se muestra en la figura, y penetra una distancia de 6 cm antes de detenerse. Calcule la fuerza de frenado F, si la velocidad de entrada fue de 80 m/s.

Se tienen como datos la rapidez inicial y la rapidez final, además de la masa de la bala como la cantidad desplazada mientras se le aplica la fuerza. Por el teorema del trabajo y la energía se puede encontrar el valor de esa fuerza:

La rapidez v(2) es el estado final (0 m/s), y la rapidez v(1) es el estado inicial antes de entrar al banco de fango (80 m/s). La masa de la bala es 20 g = 0.02 Kg.

energía mecánica y su conservación

Trabajo mecánico

Conservación de la energía mecánica

La energía mecánica (EM) de un cuerpo o un sistema, equivale a la suma de sus energías potencial y cinpetica, es decir:

EM = EC + EP

Es decir:

EC + EP = Constante

Esta ley es mucho más fácil comprenderla a través de un ejemplo:

Una piedra se suelta desde una altura de 2 m respecto del suelo aquí, en la superficie terrestre. Si despreciamos los efectos de roce con el aire, ¿con qué rapidez impacta en el suelo?

www.alipso.com › Apuntes y Monografías › Física

MAGNITUDES FISICAS

DEFINICIONES:

Magnitud

Una magnitud física es una propiedad o cualidad medible de un sistema físico, es decir, a la que se le pueden asignar distintos valores como resultado de una medición.

Magnitudes escolares

Las magnitudes escalares son aquellas que quedan completamente definidas por un número y las unidades utilizadas para su medida. Esto es, las magnitudes escalares están representadas por el ente matemático más simple, por un número. Podemos decir que poseen un módulo, pero que carecen de dirección. Su valor puede ser independiente del observador ( la masa, la temperatura, la densidad, etc.) o depender de la posición o estado de movimiento del observador.

Magnitudes vectoriales

Las magnitudes vectoriales son aquellas que quedan caracterizadas por una cantidad (intensidad o módulo), y una dirección. En un espacio euclidiano, de no más de tres dimensiones, un vector se representa mediante un segmento orientado. Ejemplos de estas magnitudes son: la velocidad, la aceleración, la fuerza, el campo eléctrico, intensidad luminosa, etc.

Sistema internacional de unidades

El Sistema Internacional de Unidades se basa en dos tipos de magnitudes físicas: Son longitud, tiempo, masa, intensidad de corriente eléctrica, temperatura, cantidad de sustancia e intensidad luminosa.

Las unidades derivadas, que son las restantes y que pueden ser expresadas con una combinación matemática de las anteriores.

Las magnitudes básicas no derivadas del SI son las siguientes:

Longitud: metro (m). El metro es la distancia recorrida por la luz en el vacío en 1/299 792 458 segundos.

Tiempo: segundo (s). El segundo es la duración de 9 192 631 770 períodos de la radiación correspondiente a la transición entre los dos niveles hiperfinos del estado fundamental del cesio-133

Masa: kilogramo (kg). El kilogramo es la masa de un cilindro de aleación de Platino-Iridio depositado en la Oficina Internacional de Pesas y Medidas.

Intensidad de corriente eléctrica: amperio (A). El amperio o ampere es la intensidad de una corriente constante que, manteniéndose en dos conductores paralelos, rectilíneos, de longitud infinita, de sección circular despreciable y situados a una distancia de un metro uno de otro, en el vacío, produciría una fuerza igual a 2×10-7 newton por metro de longitud.

Temperatura: kelvin (K). El kelvin es la fracción 1/273,16 de la temperatura del punto triple del agua.

Cantidad de sustancia: mol (mol). El mol es la cantidad de sustancia de un sistema que contiene tantas entidades elementales como átomos hay en 12 gramos de carbono-12.

Intensidad luminosa: candela (cd). La candela es la unidad luminosa, en una dirección dada, de una fuente que emite una radiación monocromática de frecuencia 540×1012 Hz y cuya intensidad energética en dicha dirección es 1/683 vatios por estereorradián

Análisis dimensional

El análisis dimensional es una herramienta conceptual muy utilizada en la física, la química y la ingeniería para ganar comprensión de fenómenos que involucran una combinación de diferentes cantidades físicas. Es además, rutinariamente utilizada para verificar relaciones y cálculos, así como para construir hipótesis razonables sobre situaciones complejas, que puedan ser verificadas experimentalmente. Uno de dichos usos está basado en el requerimiento de consistencia dimensional. Este requerimiento está relacionado con la 2da Ley de Newton: cuando se describen magnitudes mecánicas, el conjunto de magnitudes que se utilice puede ser arbitrario; sin embargo existen dos tipos de sistemas de magnitudes, los consistentes y los no consistentes. Se dirá que un sistema de magnitudes es consistente si las magnitudes que lo define verifican la siguiente propiedad

[F] = [M][A]

Vectores

DEFINICIÓN: Es un segmento de recta orientado, que sirve para representar las magnitudes vectoriales.

Igualdad de vectores

Definición:

Dos vectores y son iguales, = , si tienen la misma magnitud y la misma dirección.

Ejemplo:

Suma de vectores coliniales

Si tienen la misma dirección.

Por ejemplo: Tenemos dos muchachos jalando un solo cordón para poder arrastrar un vehículo con llantas. Uno tira con 400 N y el otro con 600 N hacia la derecha. Como los dos muchachos jalan en el mismo sentido, la fuerza total, o resultante es de 1000 N. Los vectores se suman.

Resta de vectores coliniales

Para restar dos vectores libres y se suma con el opuesto de los vectores. Las componentes del vector resta se obtienen restando las componentes de los vectores.

Movimiento en dos dimensiones

Sistema de referencia

Un sistema de referencia o marco de referencia es un conjunto de convenciones usadas por un observador para poder medir la posición y otras magnitudes físicas de un objeto o sistema físico en el tiempo y el espacio.

Partícula

Una partícula de un cuerpo es la menor porción de materia de ese cuerpo que conserva sus propiedades químicas. Pueden ser átomos, iones, moléculas o pequeños grupos de las anteriores especies químicas. Física de partículas, parte de la Física que estudia los componentes elementales de la materia y las interacciones entre ellos.

Trayectoria

Se llama trayectoria a la sucesión de puntos por los que pasó el movil en su recorrido y su valor en el Sistema Internacional es esa distancia, medida sobre la trayectoria, normalmente irregular, en metros.

Desplazamiento

es la longitud de la trayectoria comprendida entre la posición inicial y la posición final de un punto material. Un caso particular de desplazamiento es el debido a la difusión.

Velocidad

La velocidad es una magnitud física de carácter vectorial que expresa la distancia recorrida por un objeto por unidad de tiempo. Se representa por o . Sus dimensiones son [L]/[T]. Su unidad en el Sistema Internacional es el m/s.

Rapidez

La rapidez promedio o celeridad promedio es la relación entre la distancia recorrida y el tiempo empleado en recorrerla. Su magnitud se designa como v. La celeridad es una magnitud escalar con dimensiones de [L]/[T]. La rapidez se mide en las mismas unidades que la velocidad, pero no tiene el carácter vectorial de ésta. La celeridad instantánea representa justamente el módulo de la velocidad instantánea.

Movimiento unidimensional con velocidad constante

El Movimiento rectilíneo uniformemente acelerado (MRUA), también conocido como Movimiento rectilíneo uniformemente variado (MRUV) y Movimiento Unidimensional con Aceleración Constante, es aquél en el que un móvil se desplaza sobre una trayectoria recta y está sometido a una aceleración constante. Esto implica que para cualquier intervalo de tiempo, la aceleración del móvil tendrá siempre el mismo valor.

Graficas de la función de posición, tiempo y de la función velocidad, tiempo y aceleración

Espacio (distancia o desplazamiento) en función del tiempo

El espacio (distancia o desplazamiento) recorrido en un Movimiento Uniformemente Acelerado (MUA) puede representarse en función del tiempo. La gráfica es una parábola cóncava ascendent

Velocidad en función del tiempo

En un Movimiento Uniformemente Acelerado (MUA) la velocidad varía proporcionalmente al tiempo, por lo que la representación gráfica v-t (velocidad en función del tiempo) es una recta ascendente.

Aceleración en función del tiempo

Tal como lo dice su nombre, en el Movimiento uniformemente acelerado la aceleración es constante, por lo que la gráfica a-t (aceleración en función del tiempo) es una recta paralela al eje del tiempo, por encima de esta (la fuerza responsable de la aceleración es constante).

Movimiento en dos dimensiones

Movimiento bidimensional con aceleración constante

Consideremos el movimiento de una partícula en un plano, durante el cual la magnitud y la dirección de la aceleración permanecen constantes. Es decir, x a y y a no cambian con respecto al tiempo. El movimiento de una partícula en el plano puede determinarse por medio de su vector de posición r. El vector de posición para una partícula que se mueve en el plano xy puede escribirse como.

Movimiento constante

Un movimiento es rectilíneo cuando el cuerpo describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula. Nos referimos a él mediante el acrónimo MRU.

Movimiento compuesto

Cuando un cuerpo sigue un movimiento compuesto por dos movimientos simples y simultáneos, su posición en un tiempo dado es independiente de cómo actúen los movimientos simples, simultánea o sucesivamente".

Movimiento semiparabólico

El movimiento de parábola o semiparabólico (lanzamiento horizontal) se puede considerar como la composición de un avance horizontal rectilíneo uniforme y la caída libre de un cuerpo en reposo. El movimiento semiparabólico es el movimiento horizontal que realizan diferentes objetos, el ejemplo más claro de este movimiento es el lanzamiento de un proyectil, parte con una velocidad 0.

Movimiento parabólico

El movimiento parabólico completo se puede considerar como la composición de un avance horizontal rectilíneo uniforme y un lanzamiento vertical hacia arriba, que es un movimiento rectilíneo uniformemente acelerado hacia abajo (MRUA) por la acción de la gravedad

Movimiento Circular Uniforme

En física, el movimiento circular uniforme describe el movimiento de un cuerpo atravesando, con rapidez constante, una trayectoria circular. Aunque la rapidez del objeto es constante, su velocidad no lo es: La velocidad, una magnitud vectorial, tangente a la trayectoria, en cada instante cambia de dirección. Esta circunstancia implica la existencia de una aceleración que, si bien en este caso no varía al módulo de la velocidad, sí varía su dirección.

Desplazamiento angular

ES LA DISTANCIA RECORRIDA POR UN CUERPO QUE SIGUE UNA TRAYECTORIA CIRCULAR Y SE EXPRESA FRECUENTEMENTE EN RADIANES (RAD) GRADOS (º) CICLOS (C) Y REVOLUCIONES (REV);DE ESTAS UNIDADES EL RADIN ES EL MAS UTILIZADO. PUESTO QUE LA CIRCUNFERENCIA ENTERA DE UN CIRCULO ES PRECISAMENTE 2 PI VESES EL RADIO EN UN CIRCULO COMPLETO HAY 2 PI RAD.

Velocidad Angular

La velocidad angular es una medida de la velocidad de rotación. Se define como el ángulo girado por una unidad de tiempo y se designa mediante la letra griega ω. Su unidad en el Sistema Internacional es el radián por segundo (rad/s).

Aunque se la define para el movimiento de rotación del sólido rígido, también se la emplea en la cinemática de la partícula o punto material, especialmente cuando esta se mueve sobre una trayectoria cerrada

Aceleración angular

Se define la aceleración angular como el cambio que experimenta la velocidad angular por unidad de tiempo. Se denota por la letra griega alfa . Al igual que la velocidad angular, la aceleración angular tiene carácter vectorial.

Movimiento circular con aceleración angular constante

Este movimiento ocurre sobre una circunferencia, pero se diferencia del anterior en que la velocidad tangencial aumenta uniformemente a medida que la partícula recorre la circunferencia. Como se ve en la figura, a medida que pasa el tiempo, la velocidad tangencial aumenta, esto es debido a que la velocidad angular w aumenta uniformemente a medida que se recorre la circunferencia, este cambio genera una aceleración angular g definida a continuación. La aceleración total es la suma vectorial de la aceleración centrípeta y la aceleración angular.

Estática

Equilibrio

Situación que se da en un sistema físico (es decir, un sistema al que podemos atribuir una energía interna) cuando todos los factores exteriores y/o procesos internos no producen cambios de presión, temperatura u otras variables.

Primera condición de equilibrio

Un cuerpo se encuentra en estado de equilibrio trasnacional si y sólo si la suma vectorial de las fuerzas que actúan sobre él es igual a cero. Cuando un cuerpo está en equilibrio, la resultante de todas las fuerzas que actúan sobre él es cero. En este caso, Rx como Ry debe ser cero; es la condición para que un cuerpo esté en equilibrio.

Momento de una fuerza (torque)

En mecánica newtoniana, se denomina momento de una fuerza (respecto a un punto dado) a una magnitud (pseudo)vectorial, obtenida como producto vectorial del vector de posición del punto de aplicación de la fuerza con respecto al punto al cual se toma el momento por la fuerza, en ese orden. También se le denomina momento dinámico o sencillamente momento. Ocasionalmente recibe el nombre de torque a partir del término inglés (torque), derivado a su vez del latín torquere (retorcer). Este término intenta introducirse en la terminología española, bajo las formas de torque o torca, aunque con escasa fortuna, ya que existe la denominación par que es la correcta en español.

Segunda condición de equilibrio

La estática es la rama de la mecánica clásica que analiza las cargas (fuerza, par / momento) y estudia el equilibrio de fuerzas en los sistemas físicos en equilibrio estático, es decir, en un estado en el que las posiciones relativas de los subsistemas no varían con el tiempo. La primera ley de Newton implica que la red de la fuerza y el par neto (también conocido como momento de fuerza) de cada organismo en el sistema es igual a cero. De esta limitación pueden derivarse cantidades como la carga o la presión. La red de fuerzas de igual a cero se conoce como la primera condición de equilibrio, y el par neto igual a cero se conoce como la segunda condición de equilibrio.

Dinámica

Leyes del movimiento de Newton

La primera ley del movimiento rebate la idea aristotélica de que un cuerpo sólo puede mantenerse en movimiento si se le aplica una fuerza. Newton expone que: Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él.

Esta ley postula, por tanto, que un cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuyo resultante no sea nulo sobre él. Newton toma en cuenta, así, el que los cuerpos en movimiento están sometidos constantemente a fuerzas de roce o fricción, que los frena de forma progresiva, algo novedoso respecto de concepciones anteriores que entendían que el movimiento o la detención de un cuerpo se debía exclusivamente a si se ejercía sobre ellos una fuerza, pero nunca entendiendo como esta a la fricción. En consecuencia, un cuerpo con movimiento rectilíneo uniforme implica que no existe ninguna fuerza externa neta o, dicho de otra forma; un objeto en movimiento no se detiene de forma natural si no se aplica una fuerza sobre él. En el caso de los cuerpos en reposo, se entiende que su velocidad es cero, por lo que si esta cambia es porque sobre ese cuerpo se ha ejercido una fuerza neta.

Ejemplo, para un pasajero de un tren, el interventor viene caminando lentamente por el pasillo del tren, mientras que para alguien que ve pasar el tren desde el andén de una estación, el interventor se está moviendo a una gran velocidad. Se necesita, por tanto, un sistema de referencia al cual referir el movimiento.

Segunda ley

La segunda ley del movimiento de Newton dice que El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime. Esta ley explica qué ocurre si sobre un cuerpo en movimiento (cuya masa no tiene por qué ser constante) actúa una fuerza neta: la fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. En concreto, los cambios experimentados en el momento lineal de un cuerpo son proporcionales a la fuerza motriz y se desarrollan en la dirección de esta; esto es, las fuerzas son causas que producen aceleraciones en los cuerpos. Consecuentemente, hay relación entre la causa y el efecto, esto es, la fuerza y la aceleración están relacionadas. Dicho sintéticamente, la fuerza se define simplemente en función del momento en que se aplica a un objeto, con lo que dos fuerzas serán iguales si causan la misma tasa de cambio en el momento del objeto.

Tercera ley de Newton o Ley de acción y reacción

Con toda acción ocurre siempre una reacción igual y contraria: o sea, las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto. La tercera ley es completamente original de Newton (pues las dos primeras ya habían sido propuestas de otras maneras por Galileo, Hooke y Huygens) y hace de las leyes de la mecánica un conjunto lógico y completo. Expone que por cada fuerza que actúa sobre un cuerpo (empuje), este realiza una fuerza de igual intensidad, pero de sentido contrario sobre el cuerpo que la produjo. Dicho de otra forma, las fuerzas, situadas sobre la misma recta, siempre se presentan en pares de igual magnitud y de dirección, pero con sentido opuesto. Este principio presupone que la interacción entre dos partículas se propaga instantáneamente en el espacio (lo cual requeriría velocidad infinita), y en su formulación original no es válido para fuerzas electromagnéticas puesto que estas no se propagan por el espacio de modo instantáneo sino que lo hacen a velocidad finita "c".

Es importante observar que este principio de acción y reacción relaciona dos fuerzas que no están aplicadas al mismo cuerpo, produciendo en ellos aceleraciones diferentes, según sean sus masas. Por lo demás, cada una de esas fuerzas obedece por separado a la segunda ley. Junto con las anteriores leyes, ésta permite enunciar los principios de conservación del momento lineal y del momento angular.

Fuerza

En física, la fuerza es una magnitud física que mide la intensidad del intercambio de momento lineal entre dos partículas o sistemas de partículas (en lenguaje de la física de partículas se habla de interacción). Según una definición clásica, fuerza es todo agente capaz de modificar la cantidad de movimiento o la forma de los cuerpos materiales. No debe confundirse con los conceptos de esfuerzo o de energía. En el Sistema Internacional de Unidades, la fuerza se mide en newtons (N).

Masa inercial

En física, la masa inercial o masa inerte es una medida de la resistencia de una masa al cambio de velocidad en relación con un sistema de referencia inercial. En física clásica la masa inercial de partículas puntuales se define mediante la siguiente ecuación:

Peso

En física clásica, el peso es la fuerza con la cual un cuerpo actúa sobre un punto de apoyo, y que está originada por la acción del campo gravitatorio local sobre la masa del cuerpo. Por ser una fuerza, el peso se representa como un vector, definido por su módulo, dirección y sentido, aplicado en el centro de gravedad del cuerpo y dirigido aproximadamente hacia el centro de la Tierra.

Fuerza de la fricción

La fuerza de fricción se da a partir del contacto entre dos cuerpos. En realidad, éste efecto siempre está presente en el movimiento de un cuerpo debido a que siempre se desplaza haciendo contacto con otro (el aire en la mayoría de los casos); en algunos casos, éste efecto es muy pequeño y es una buena aproximación despreciar su valor, pero en otros, es necesario tomar en cuenta ésta fuerza, debido a que determina el valor del movimiento.

Segunda ley de newton Segunda Ley de Newton aplicada al Movimiento Circular Uniforme.

Movimiento circular no uniforme. Movimiento en marcos de referencia acelerados. Movimiento en presencia de fuerzas resistivas. Modelado numérico en dinámicas de partículas. Las fuerzas fundamentales de la naturaleza aplicada al movimiento circular